Multivariate Visualizations
Announcements
Assignment 3 due tomorrow @ 11:59pm!
Tidy Tuesday 3 due Friday @ 11:59pm
Learning Goals
- Understand how we can use additional aesthetics such as color and size to incorporate a third (or more variables) to a bivariate plot
- Develop comfort with interpreting heat maps and star plots, which allow you to look for patterns in variation in many variables.
Template File
Download a template .Rmd of this activity. Put the file in a Day_05 folder within your COMP_STAT_112 folder.
- This .Rmd only contains exercises that we’ll work on in class and you’ll finish for Assignment 4.
More Aesthetic Attributes
To go beyond 2 variables, we need to add aesthetics for each new variable!
Data: Exploring SAT Scores
Though far from a perfect assessment of academic preparedness, SAT scores have historically been used as one measurement of a state’s education system.
| State | expend | ratio | salary | frac | verbal | math | sat | fracCat |
|---|---|---|---|---|---|---|---|---|
| Alabama | 4.405 | 17.2 | 31.144 | 8 | 491 | 538 | 1029 | (0,15] |
| Alaska | 8.963 | 17.6 | 47.951 | 47 | 445 | 489 | 934 | (45,100] |
| Arizona | 4.778 | 19.3 | 32.175 | 27 | 448 | 496 | 944 | (15,45] |
| Arkansas | 4.459 | 17.1 | 28.934 | 6 | 482 | 523 | 1005 | (0,15] |
| California | 4.992 | 24.0 | 41.078 | 45 | 417 | 485 | 902 | (15,45] |
| Colorado | 5.443 | 18.4 | 34.571 | 29 | 462 | 518 | 980 | (15,45] |
Data: Codebook
Univariate Density
Variability in average SAT scores from state to state:
Bivariate Scatterplot
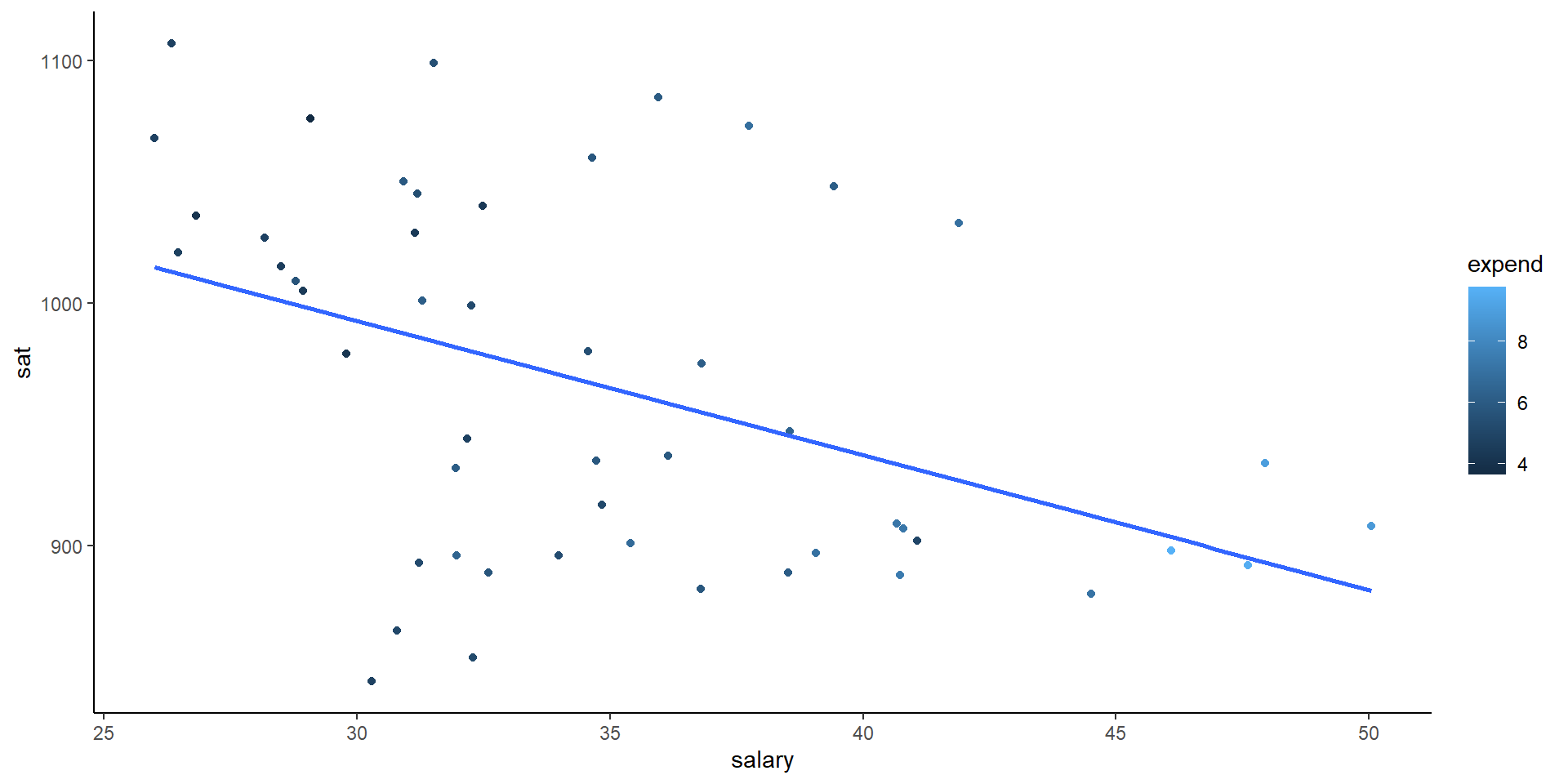
What degree do per pupil spending (expend) and teacher salary explain this variability?
ggplot(education, aes(y = sat, x = salary)) +
geom_point() +
geom_smooth(se = FALSE, method = "lm") + theme_classic()
ggplot(education, aes(y = sat, x = expend)) +
geom_point() +
geom_smooth(se = FALSE, method = "lm") + theme_classic()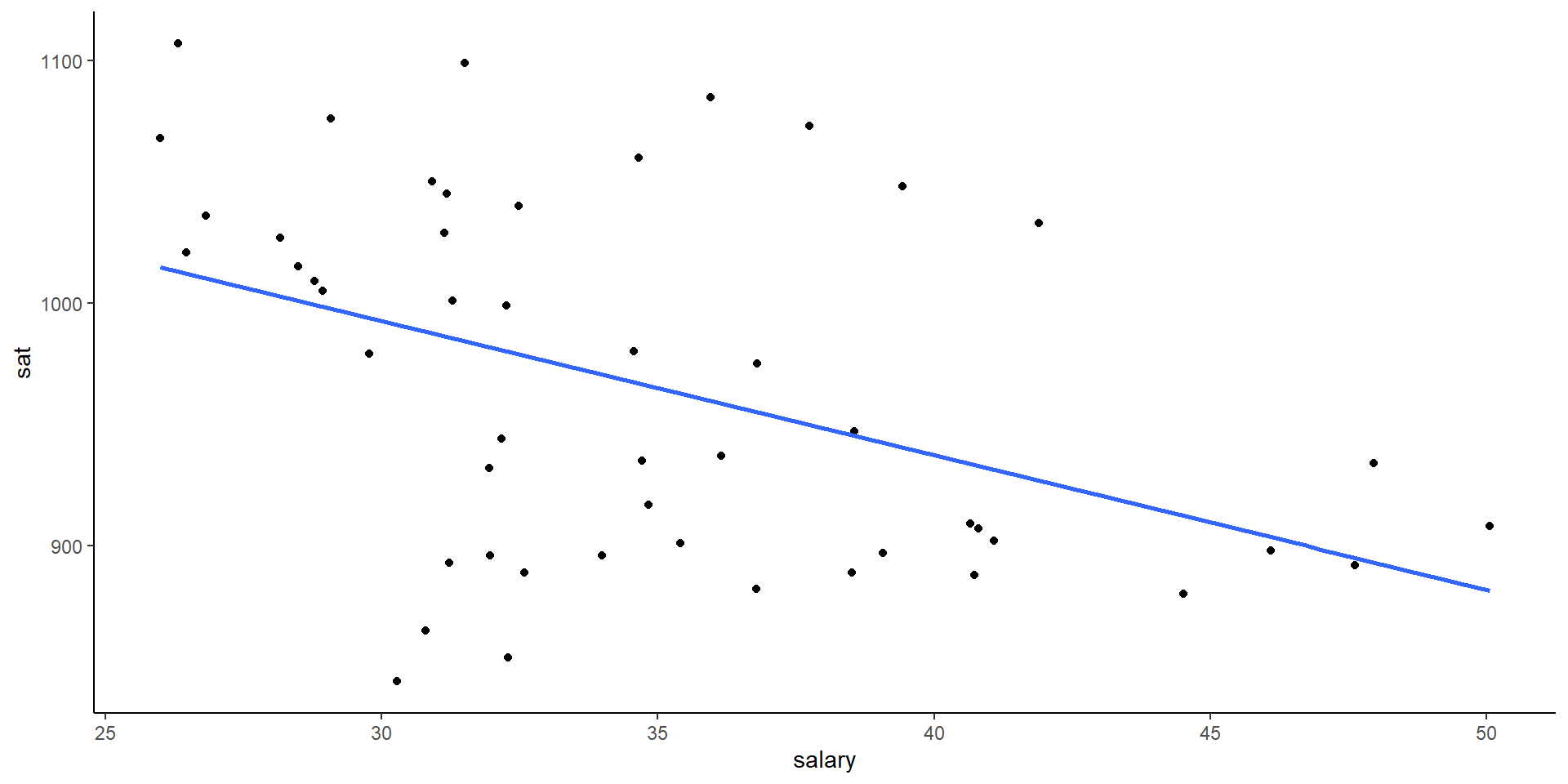
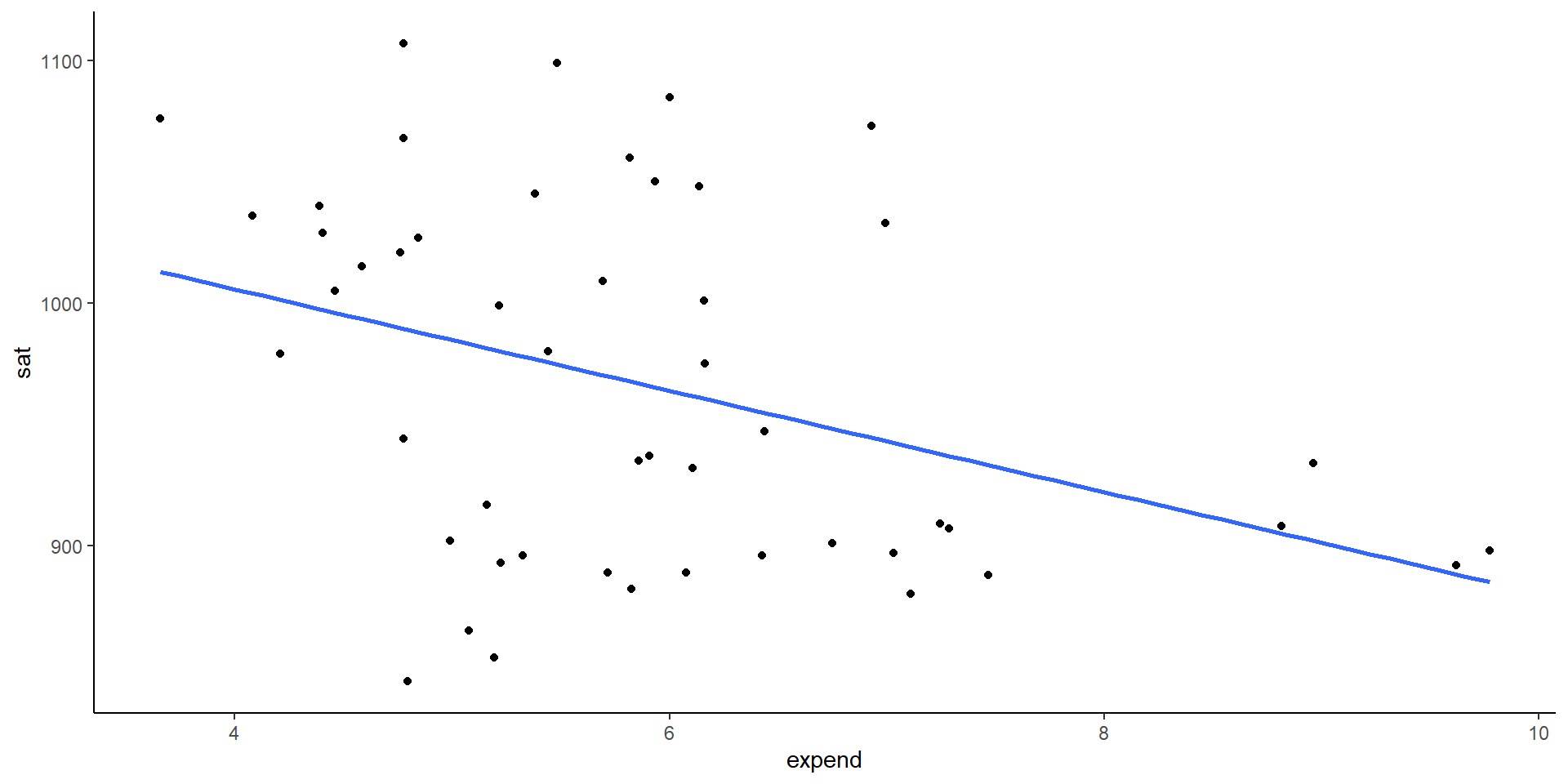
Is there anything that surprises you in the above plots? What are the relationship trends? Discuss as a group and write down your thoughts in Rmd.
Exercise: Three Variables
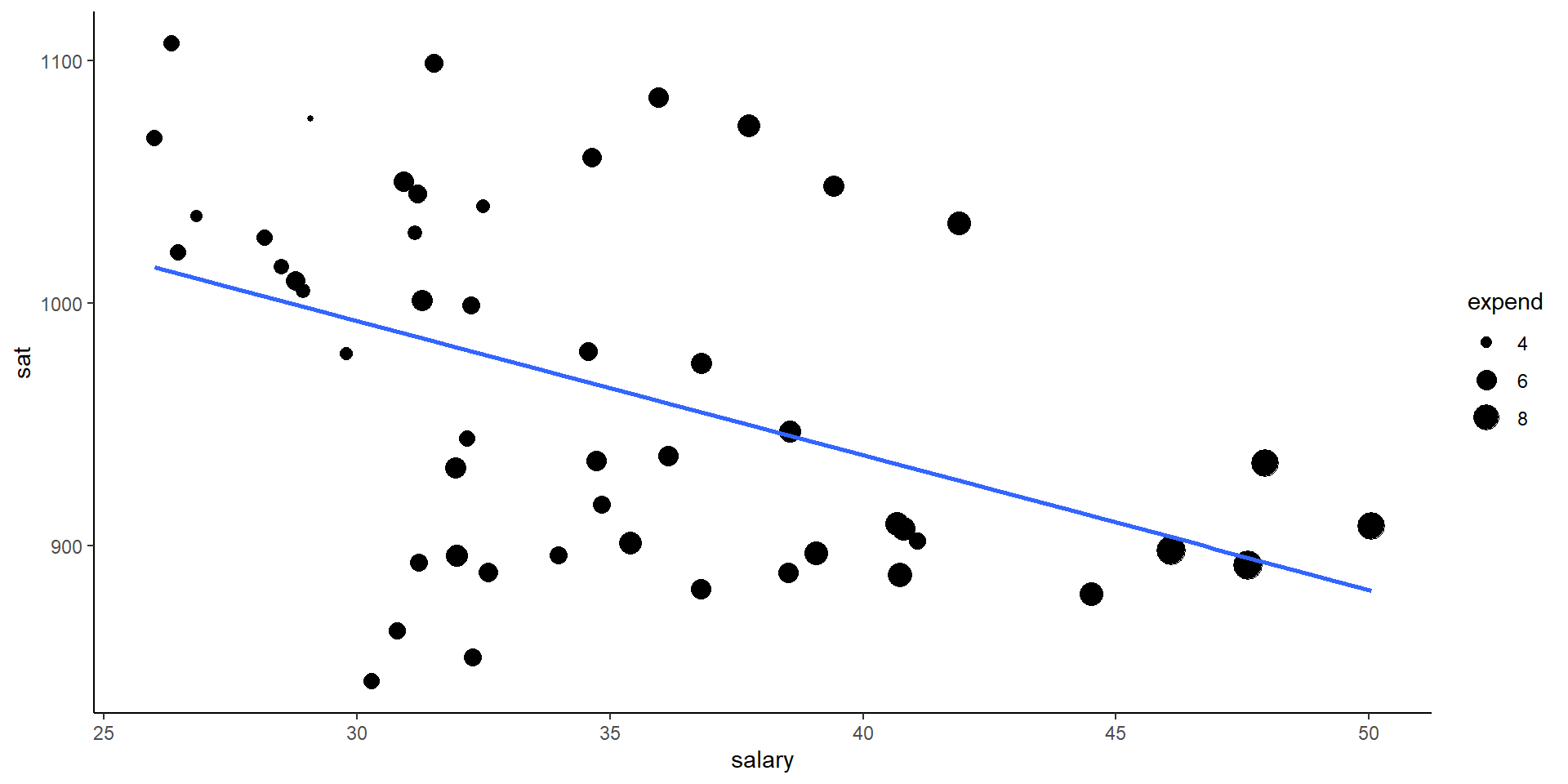
Make a single scatterplot visualization that demonstrates the relationship between sat, salary, and expend.
Hints:
1. Try using the color or size aesthetics to incorporate the expenditure data.
2. Include some model smooths with geom_smooth() to help highlight the trends.
Exercise: Three Variables
Another option!
Categorize your 3rd Quantitative Variable!
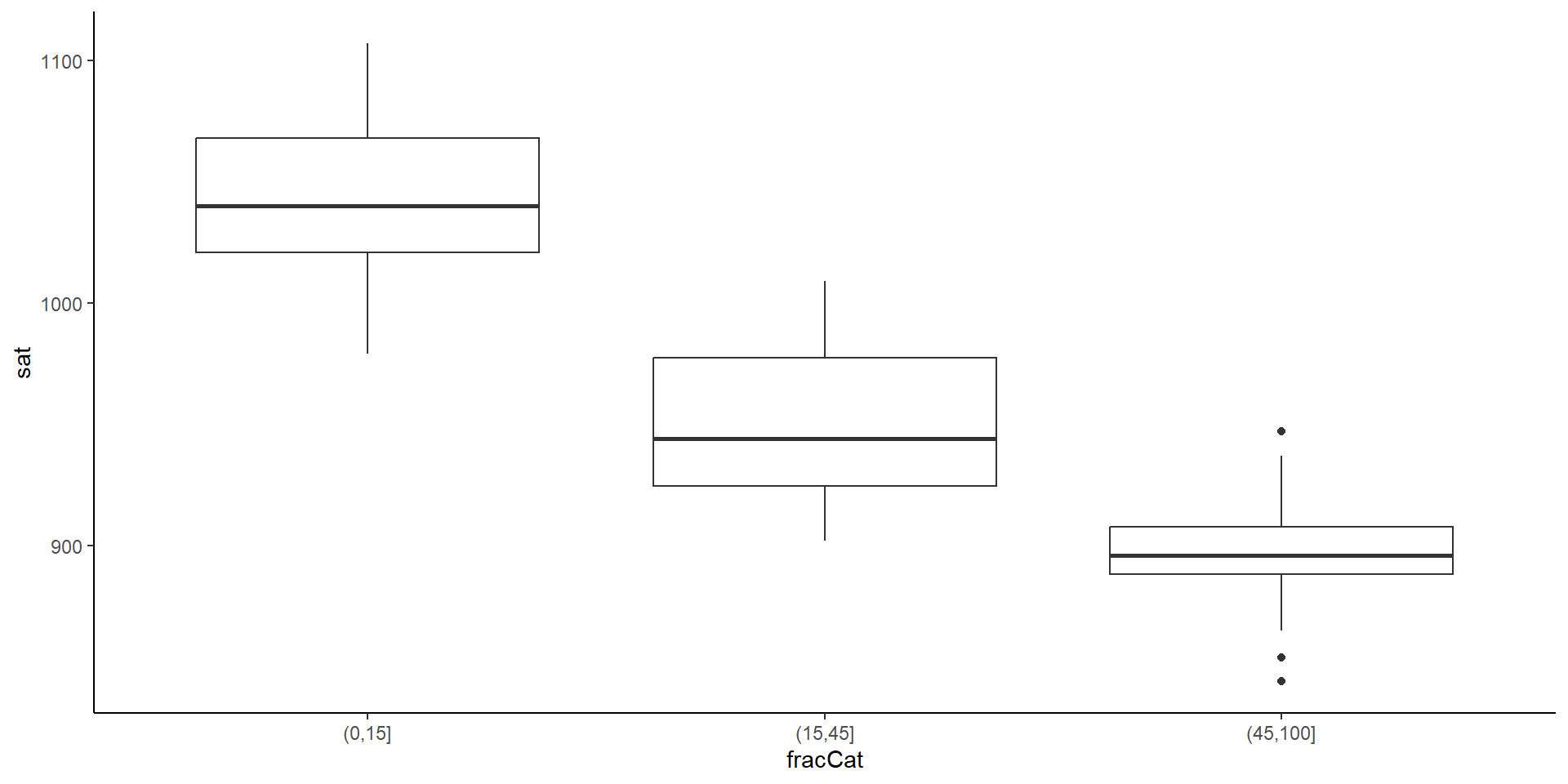
Exercise: Fraction who take SAT
The fracCat variable in the education data categorizes the fraction of the state’s students that take the SAT into low (below 15%), medium (15-45%), and high (at least 45%).
- Make a univariate visualization of the
fracCatvariable to better understand how many states fall into each category.
Exercise: Fraction who take SAT
- Make a bivariate visualization that demonstrates the relationship between
fracCatandsat. What story does your graphic tell?
Exercise: Fraction who take SAT
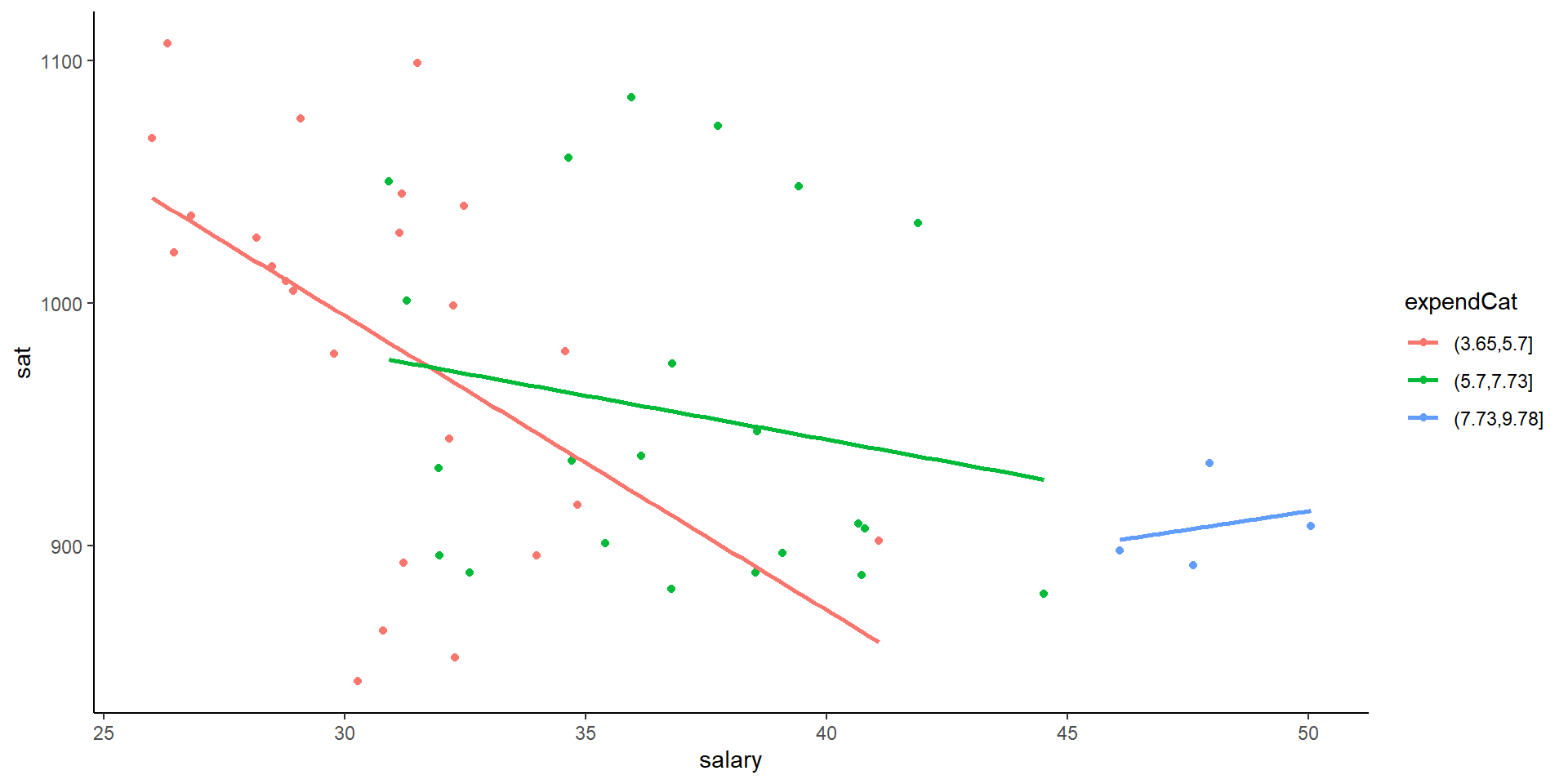
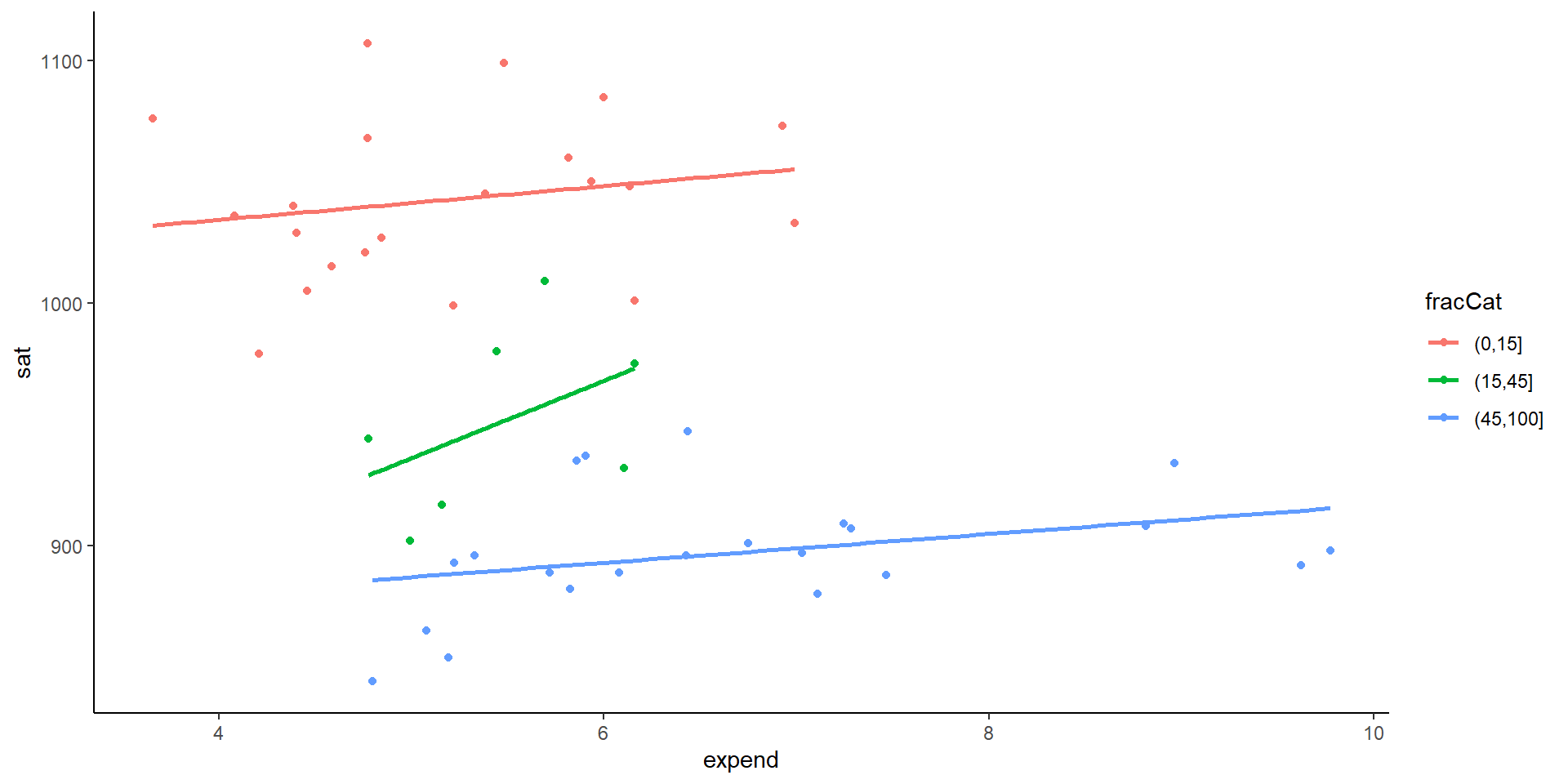
- Make a trivariate visualization that demonstrates the relationship between
fracCat,sat, andexpend. IncorporatefracCatas the color of each point, and use a single call togeom_smoothto add three trendlines (one for eachfracCat). What story does your graphic tell?
Exercise: Fraction who take SAT
- Putting all of this together, explain this example of Simpson’s Paradox. That is, why does it appear that SAT scores decrease as spending increases even though the opposite is true?
Discuss!
Other Multivariate Visualization Techniques
Heat maps
Note that each variable (column) is scaled to indicate states (rows) with high values (yellow) to low values (purple/blue).
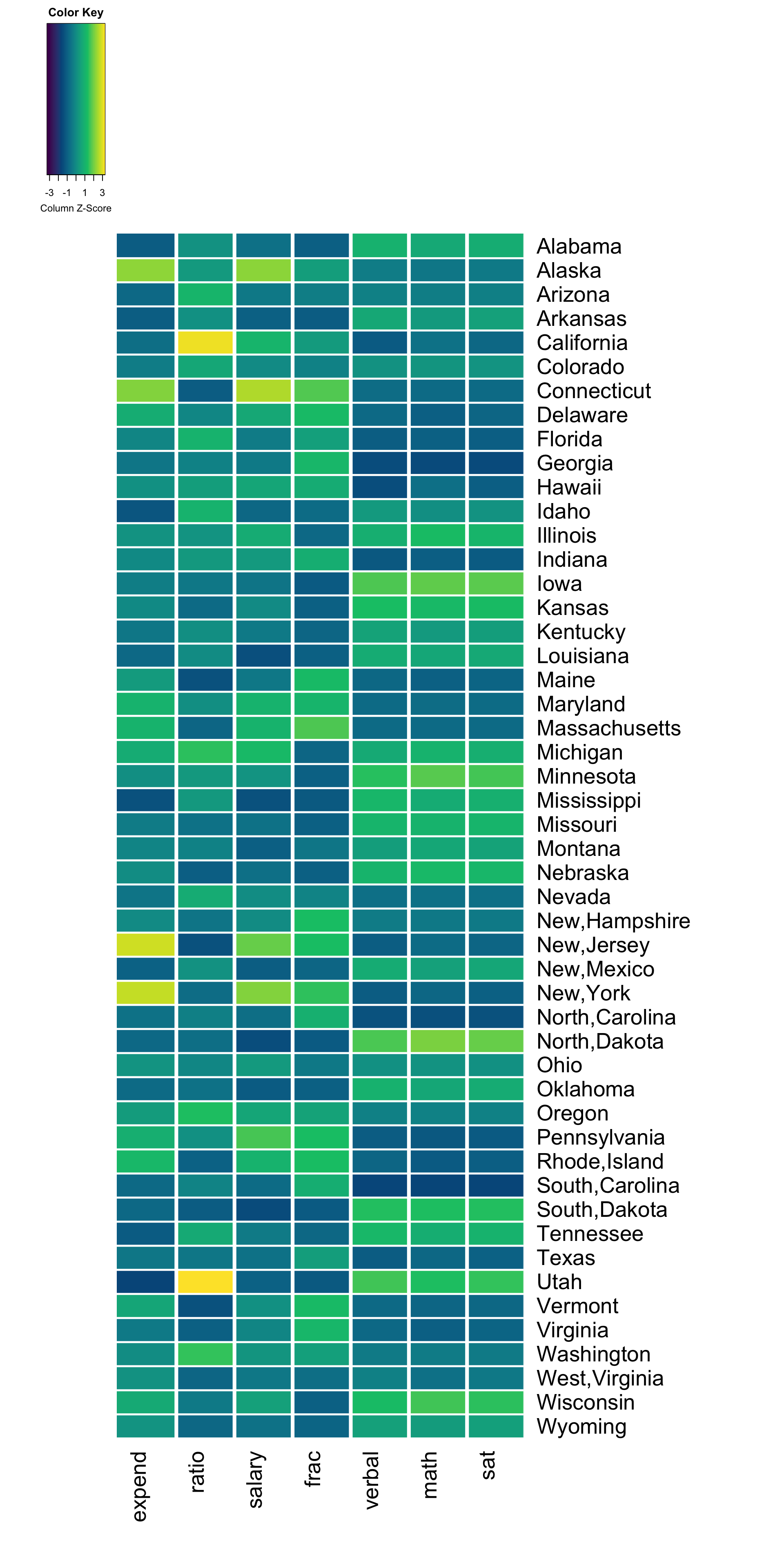
What do you notice? What insight do you gain about the variation across U.S. states?
Heat maps with Row Cluster
Include dendrograms helps to identify interesting clusters.
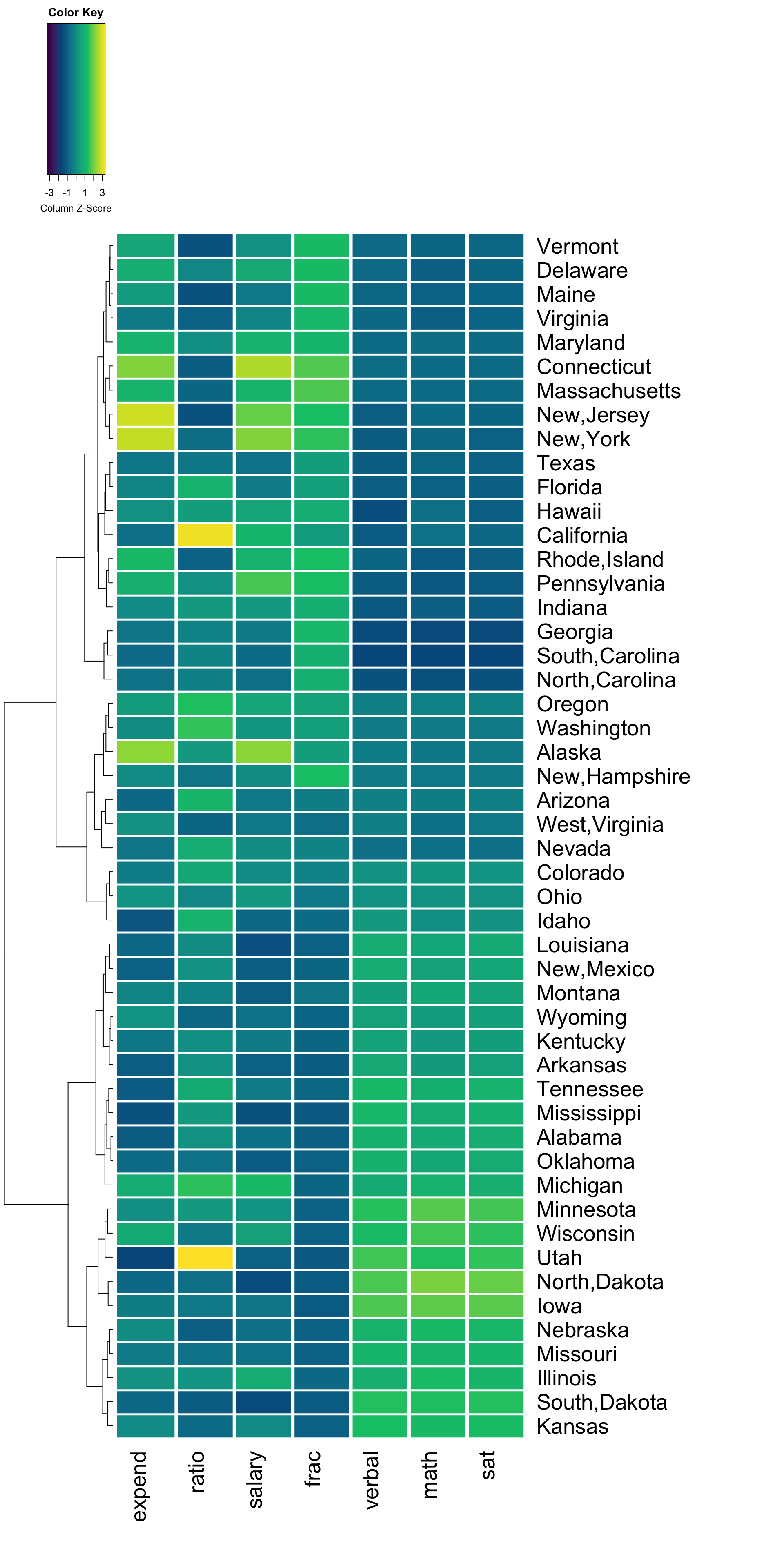
What do you notice? What new insight do you gain about the variation across U.S. states, now that states are grouped and ordered to represent similarity?
Heat maps with Column Cluster
We can also construct a heat map which identifies interesting clusters of columns (variables).
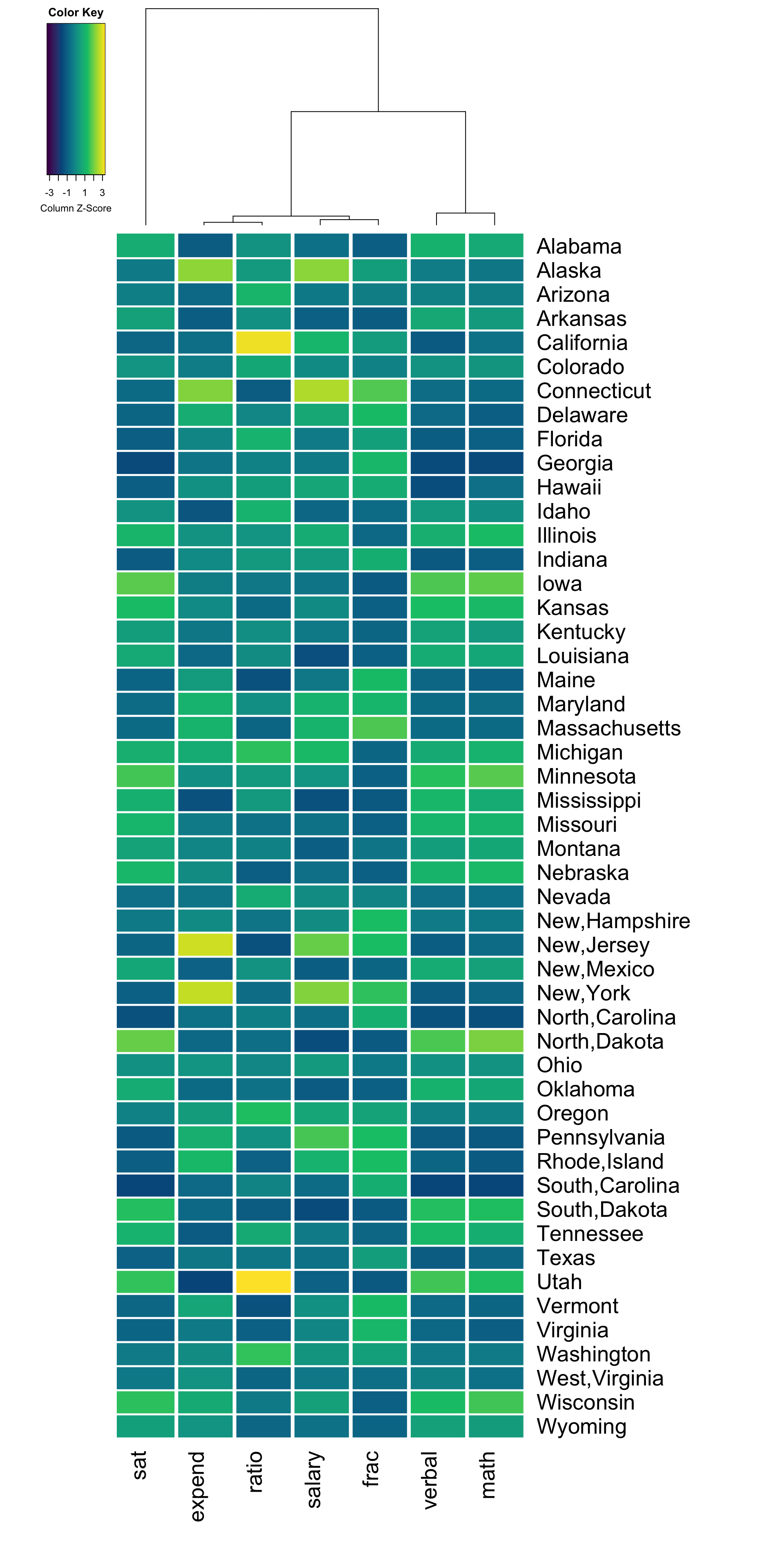
What do you notice? What new insight do you gain about the variation across U.S. states, now that variables are grouped and ordered to represent similarity?
Star plots
Star plot visualizations indicate the relative scale of each variable for each state.

What do you notice? What new insight do you gain about the variation across U.S. states with the star plots?
Star plots
Star plot visualizations indicate the relative scale of each variable for each state.